1. 정렬의 소개
*리스트 연산
- 리스트에 원소를 추가 또는 제거하고 원하는 원소를 검색
- 제약점 -> 정렬된 리스트만을 요구함
- 정렬되지 않은 리스트라면? -> 정렬
* 정렬 (sorting)
- 데이터를 정해진 키에 따라서 크기 순으로 배열하는 것
- 오름차순 (ascending order)
- 내림차순 (descending order)
*정렬 알고리즘의 성능
- 정렬할 데이터의 개수 : n
- O(f(n))으로 표시
- O(n^2)정렬 알고리즘 - 버블정렬, 삽입 정렬, 선택 정렬, ....
- O(nlogn) 정렬 알고리즘 - 합병 정렬, 쾌속 정렬, ....
2. O(n^2) 정렬
- 정렬 알고리즘의 성능은 정렬하고자 하는 원소의 수 (n)의 제곱인 (n^2)에 비례함.
- 이동에 기반한 정렬 : 삽입 정렬
- 교환에 기반한 정렬 : 버블 정렬 , 선택 정렬
2-1. 삽입 정렬
* 기본 원리
- 추가 (insert) 연산에 기반한 정렬 알고리즘
- 정렬되지 않은 리스트의 원소들을 차례로 정렬된 리스트에 추가하면 정렬이 수행됨
- 원소를 이동시켜서 정렬을 수행함
* 알고리즘 설계
- 배열의 원소를 하나씩 부분 배열에 삽입하면서 정렬을 수행
- 정렬이 끝난 배열의 앞부분을 부분 배열로 이용
* 알고리즘 구현

* 성능 분석
- insert() 의 수행 시간 -> O(n)
- insert() 를 호출하는 횟수 -> O(n)
- 결과 : O(n^2)
2-2. 버블 정렬
* 기본 원리
- 교환을 통해서 더 작은 원소를 앞으로 보냄
- 서로 인접한 원소들 사이의 교환을 반복해서 정렬을 수행함

* 기본 개념
- 배열의 가장 앞자리에 최소값을 옮김
- 배열의 두 번째 자리에 두 번째 작은 값을 옮김
- 이 과정을 n-1 번 반복함
- 마치 거품(bubble)이 물밑에서 올라오는 듯 함
- sinking sort라고도 함
* 알고리즘 구현


* 성능 분석
- 안쪽 for-loop의 수행 횟수 = n(n-1)/2 = O(n^2)
* 버블 정렬의 단점
- 최악의 경우 O(n^2)번의 교환을 수행해야 함
* 버블 정렬의 단점을 개선 -> 선택 정렬 (selection sort)
- 최악의 경우에도 O(n)번만 교환하는 정렬은 없을까?
- i 번째 자리에 올 원소는 i번째로 작은 원소
- i 번째로 작은 원소를 찾아서 i번째 원소와 교환
2-2. 선택 정렬 (selection sort)
* 기본 개념
- 배열의 첫 번째 자리에 최소값을 옮김
- 배열의 두 번째 자리에 두 번째 작은 값을 옮김
- 이 과정 반복
- select_min()함수 사용
* 알고리즘 설계
- 정렬하고자 하는 배열의 첫 번째 원소부터 차례로 방문
* 알고리즘 구현

* 성능 분석
- select_min() -> n개에 대해서 수행 -> O(n)
- select_min () 함수를 O(n)번 수행
- 결과 : O(n^2)
3. O(nlogn) 정렬
- 원소들 사이의 비교(O(n^2))를 지양
- 분할 정복 방식 (divide & conquer) 추구 - 합병 정렬 , 쾌속 정렬
- 트리 구조를 이용 (힙 정렬)
* 분할 정복의 3단계
- 주어진 집합의 데이터를 적절한 크기의 부분 집합으로 나눔 -> 분할
- 부분 집합에서 문제를 해결 -> 정복
- 해결된 부분 해를 합쳐서 주어진 집합의 해를 구함 -> 결합
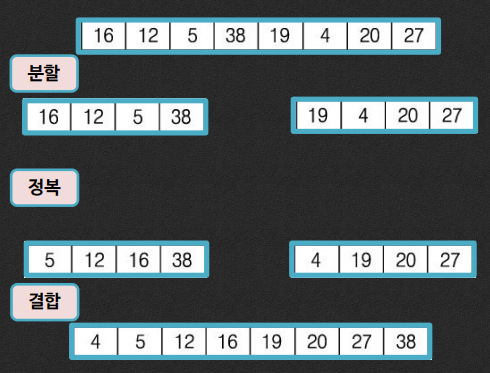
3-1. 합병 정렬
* 합병 정렬의 원리
- 분할
- n 개의 원소를 가진 배열을 2개로 분할
- 더 이상 분할할 수 없을 때까지 분할을 반복
- 정복
- 더 이상 분할할 수 없는 배열은 정렬된 것으로 간주
- 결합
- 정렬된 배열을 합병해서 더 큰 정렬된 배열을 생성
- n 개의 원소를 가진 정렬된 배열까지 합병을 계속
* 합병 정렬 알고리즘


* 시간 복잡도
- 분할 - O(n)
- 정복 - O(1)
- 결합 - O(nlog)
- 결론 : O(nlogn)
3-2. 쾌속 정렬
- 분할 정복 구조의 정렬 알고리즘
- 결합을 요구하지 않는 분할 정복 구조
- 리스트를 적절하게 분할해서 결합의 필요성 제거
*합병 정렬과 비교

*분할 알고리즘


* 쾌속 정렬과 합병 정렬의 성능 비교 - 시간 복잡도
| 예 | 쾌속 정렬 | 합병 정렬 | |
| Best case | 5 1 6 3 4 8 7 2 | O(nlogn) | O(nlogn) |
| Worst case | 1 2 3 4 5 6 7 8 | O(n^2) | O(nlogn) |
| Average case | 4 1 3 6 5 2 9 8 | O(nlogn) | O(nlogn) |
평균적으로는 쾌속 정렬이 합병 정렬보다 성능이 뛰어나다고 알려져 있음
*결론
- 단순한 정렬 알고리즘 : O(n^2) 성능 - 버블 정렬, 삽입 정렬 , 선택 정렬
- 분할정복 정렬 알고리즘 : O(nlogn) 성능 - 합병 정렬, 쾌속 정렬
- 성능 차이가 크기 때문에 분할정복 정렬 알고리즘을 사용하는게 유리
'자료구조 C++' 카테고리의 다른 글
| 9. 우선 순위 큐 (Heap) (0) | 2021.02.07 |
|---|---|
| 8. 이진 탐색 트리 (binary search tree) (0) | 2021.02.03 |
| 7. 트리(tree) (0) | 2021.02.03 |
| 4. 연결 리스트 (linked list) (0) | 2021.02.03 |
| 3. 배열 (Array) (0) | 2021.02.03 |



