1. 개요
*배열 , 연결 리스트 , 스택, 큐의 공통점?
- 리스트형 자료구조
- 선형 자료구조
- 모든 원소는 인덱스에 대응
- 2개 이상의 관계를 표현하는데 한계 존재 - ex) 족보 , 파일 구조 , 의사 결정 => 계층 구조
* 계층 구조의 공통점?
- 하나의 근원(root)으로부터 파생됨
- 한 노드가 여러 개의 노드로 전파됨
- 순환하는 경로가 없음
2. 트리의 정의
- 루트(root)라는 특별한 노드가 하나 있음
- 모든 노드는 부모 자식 관계라는 1:1관계에 재귀적으로 연결되어 있음
3. 용어
- Root node : 트리의 최상위 노드 , 부모 노드가 없는 노드
- Leaf node : 자식 노드가 없는 노드
- Internal node : Leaf node가 아닌 모든 노드
- Parent node : 연결된 한 쌍의 노드들 중에서 root node에 더 가까운 노드를 다른 노드의 parent node라고 함
- Child node : 연결된 노드들 중에서 root node에서 더 먼 노드
- Sibling node : 같은 노드를 parent node로 공유하는 노드들
- Subtree : 어떤 트리의 노드를 root node로 하며 트리의 정의를 만족시키는 node와 edge들의 집합
- Degree of a node : 한 노드가 갖는 자식 노드의 개수
- Degree of a tree : 한 트리에 속한 노드들의 degree들의 최대값
- Depth of a node : Root node의 depth는 1 , Child node는 parent node의 depth+1
- Depth(height) of a tree : 한 트리에 속한 노드들의 depth들의 최대값
4. 트리의 자료구조
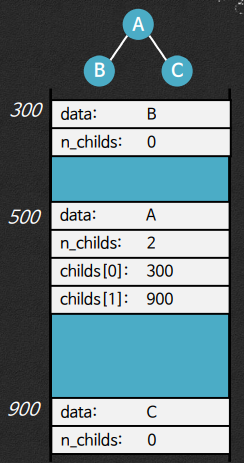
*노드
- 저장할 데이터
- 자식 노드의 수
- 자식 노드에 대한 포인터

5. 이진 트리 (binary tree)
5-1. 정의
- Degree가 2인 트리
- 모든 노드는 최대 2개의 자식 노드를 가짐
- 모든 노드가 2개의 자식 노드를 가짐 (X)
5-2. 이진 트리의 성질
- i번째 레벨의 최대 노드의 수는 2^(i-1)개
- Depth가 k인 이진 트리의 최대 노드는 2^k - 1개
5-3. 특별한 이진 트리
- 포화 이진 트리 (Full binary tree) - Depth가 k일 때 2^k - 1 개의 노드를 갖는 이진 트리
- 완전 이진 트리 (Complete binary tree) - 같은 depth를 갖는 포화 이진 트리와 노드들 사이에 1:1 대응이 성립하는 이진 트리
=> full node가 아닌 node는 반드시 두 child node가 없거나 left node만 존재, 이 후 탐색하는 node 모두 leaf node
6. 트리 탐색 (search or traversal)
- Root node로부터 시작해서 트리의 모든 노드를 방문하는 연산
- 모든 트리에서 적용되는 일반적인 탐색 - 깊이 우선 탐색 (DFS) , 넓이 우선 탐색 (BFS)
- 이진 트리에만 적용되는 특별한 탐색
* 이진 트리에서의 탐색
- 중위 우선 탐색 - 왼쪽 자식 노드 -> 부모 노드 -> 오른쪽 자식 노드
- 전위 우선 탐색 - 부모 노드 -> 왼쪽 자식 노드 -> 오른쪽 자식 노드
- 후위 우선 탐색 - 왼쪽 자식 노드 -> 오른쪽 자식 노드 -> 부모 노드
'자료구조 C++' 카테고리의 다른 글
| 9. 우선 순위 큐 (Heap) (0) | 2021.02.07 |
|---|---|
| 8. 이진 탐색 트리 (binary search tree) (0) | 2021.02.03 |
| 6. 정렬 (sorting) (0) | 2021.02.03 |
| 4. 연결 리스트 (linked list) (0) | 2021.02.03 |
| 3. 배열 (Array) (0) | 2021.02.03 |



