1. 우선 순위 큐 (Priority queue)
- 가장 우선 순위가 높은 원소가 가장 먼저 제거되는 큐
- ex) 병원 응급실
* 우선 순위 큐의 연산
- 추가 (Push)
- 큐에 새로운 원소를 삽입함
- 새로운 원소의 위치는 그 중요도(priority)에 따라서 결정됨
- 제거 (Pop)
- 큐에서 가장 우선 순위가 높은 원소를 삭제함
- 탑 (Top)
- 큐에서 가장 우선 순위가 높은 원소를 찾음(삭제하지는 않음)
* 정렬된 리스트를 이용한 우선 순위 큐의 구현의 성능
- 추가 (Push) : O(n)
- 제거 (Pop) : O(n)
- 탑 (Top) : O(1)
* 추가와 제거의 성능을 향상시킬 수 있는 방법은?
- 이진 트리를 이용!! (heap)
2. 정의
* Heap
- 이진 트리를 기반으로 구현된 우선 순위 큐
- 완전 이진 트리 (complete binary tree)
* Heap의 종류
- 최대 힙 (Max heap) : 모든 노드의 값은 자식 노도의 값들보다 작지 않음
- 최소 힙 (Min heap) : 모든 노드의 값은 자식 노드의 값들보다 크지 않음
* 최대 힙 (Max Heap)
- 정의 1) 완전 이진 트리
- 정의 2) 모든 노드의 값은 자식 노드의 값들보다 작지 않음

* 최소 힙 (Min Heap)
- 정의 1) 완전 이진 트리
- 정의 2) 모든 노드의 값은 자식 노드의 값들보다 크지 않음
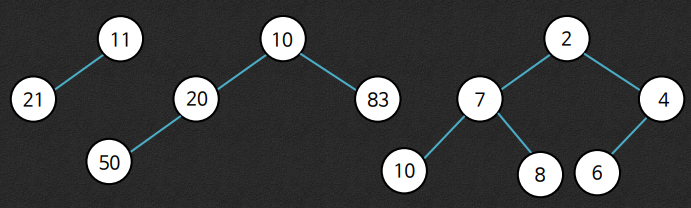
3. 힙의 구현
* 완전 이진 트리의 구현
- 포인터를 이용한 구현
- 배열을 이용한 구현

- 완전 이진 트리에서 각 노드에 위에서 아래로, 왼쪽에서 오른쪽으로 번호를 부여함
- 번호는 1부터 시작함
- 배열에서 첫 번째 원소부터 번호를 부여함
- k번째 노드의 부모 노드 : k/2
- k번째 노드의 왼쪽 child node : 2*k
- k번째 노드의 오른쪽 child node : 2*k + 1
* 힙의 자료 구조

* calloc => 메모리 동적 할당
malloc과의 차이? => malloc은 값을 초기화하지 않지만 calloc은 배열의 모든값을 0으로 초기화
* 힙의 구현 : Heapify(k) 함수
- k번쨰 노드로부터 힙을 재구성할 것
- 하향식 재구성 (Topdown heapify) : leaf node까지 힙을 재구성
- 상향식 재구성 (Bottomup heapify) : Root node까지 힙을 재구성
- ex) 하향식 재구성 (k=1)

* 하향식 재구성 (Topdown heapify)

* 상향식 재구성 (Bottomup heapify)

* Heapify의 시간 복잡도 (n개의 노드)
- 완전 이진 탐색 트리의 depth는 O(logn)임
- 최악의 경우 검색은 leaf node 또는 root node에서 끝남
- 따라서 시간 복잡도는 O(logn)
3-1. 추가 (Push)
* 최대 힙에 새로운 원소를 추가
- 원소를 힙의 마지막 위치에 삽입 -> 최대힙 정의를 만족하려면 재구성 해야함
- heapify()를 이용해서 새로운 원소가 삽입된 힙을 재구성

* 시간 복잡도
- 힙 : n개의 원소를 가진 완전 이진 트리
- 힙의 height -> log(n)
- 원소 추가 -> O(1)
- 힙의 재구성 -> O(logn)
- 추가 연산의 시간 복잡도 -> O(logn
3-2. 제거 (Pop)
* 최대 힙에서 제거
- Root node에 저장된 값을 제거
- 힙의 마지막 노드에 저장된 값을 루트 노드로 옮기고 노드를 제거
- 루트 노드로부터 하향식 힙 재구성 수행

* 시간 복잡도
- 힙 : n개의 원소를 가진 완전 이진 트리
- 힙의 height -> log(n)
- 추가 연산의 시간 복잡도 -> O(logn)
- Root node의 원소 제거 -> O(1)
- 마지막 노드 제거 -> O(1)
- 힙의 재구성 -> O(logn)
* 힙의 성능 분석
| 자료구조 | 추가 | 제거 | 검색 | 최대값 찾기 | 최대값 제거 | |
| 정렬된 배열 | O(n) | O(n) | O(logn) | O(1) | O(1) | |
| 졍렬된 연결 리스트 | O(n) | O(n) | O(n) | O(1)/O(n) | O(1)/O(n) | |
| 이진 탐색 트리 | 최선 | O(logn) | O(logn) | O(logn) | O(logn) | O(logn) |
| 최악 | O(n) | O(n) | O(n) | O(n) | O(n) | |
| Heap | O(logn) | O(logn) | - | O(1) | O(logn) | |
'자료구조 C++' 카테고리의 다른 글
| DFS와 BFS (0) | 2021.02.24 |
|---|---|
| 동적 프로그래밍(Dynamic Programming) - DP (0) | 2021.02.13 |
| 8. 이진 탐색 트리 (binary search tree) (0) | 2021.02.03 |
| 7. 트리(tree) (0) | 2021.02.03 |
| 6. 정렬 (sorting) (0) | 2021.02.03 |



